Difference between revisions of "24F Final Project: Overfitting"

Revision as of 07:27, 22 October 2022 (view source) User (talk | contribs) (→‎Recent Research) ← Older edit		Latest revision as of 07:27, 22 October 2022 (view source) User (talk | contribs) (→‎Recent Research)
(One intermediate revision by the same user not shown)
Line 9:		Line 9:
	Overfitting occurs when a machine learning model captures not only the underlying patterns in the training data, but the random noise or errors as well. This tends to happen when the model trains for too long on sample data or when the model is too complex. When a model is excessively trained on a limited dataset, it leads to the model memorizing the specific data points rather than learning the underlying patterns of the dataset.<ref name=”lark” /> Complex models with a large number of parameters are also conducive for overfitting in that they have the capacity to learn intricate details, including noise, from the training data.<ref name=”lark” />		Overfitting occurs when a machine learning model captures not only the underlying patterns in the training data, but the random noise or errors as well. This tends to happen when the model trains for too long on sample data or when the model is too complex. When a model is excessively trained on a limited dataset, it leads to the model memorizing the specific data points rather than learning the underlying patterns of the dataset.<ref name=”lark” /> Complex models with a large number of parameters are also conducive for overfitting in that they have the capacity to learn intricate details, including noise, from the training data.<ref name=”lark” />
−	With this in mind, one may logically think that ending the training process earlier, known as “early stopping,” or reducing complexity in the model would prevent overfitting; however, pausing training too early or excluding too many important features may result in the opposite problem: underfitting.<ref name=”ibm” /> Underfitting describes a model which does not capture the underlying relationship in the dataset which it was trained on.<ref name=”domino”> ''What is Underfitting in Machine Learning?'' Domino Data Lab. https://domino.ai/data-science-dictionary/underfitting</ref> While not training for long enough or being trained with poorly chosen [https://en.wikipedia.org/wiki/Hyperparameter_(machine_learning) hyperparameters] does lead to underfitting, the most common reason that models underfit is because they exhibit too much bias.<ref name=”domino” /> Basically, an underfit model will exhibit high bias and low variance, meaning it will generate reliably inaccurate predictions - while reliability is desirable, inaccuracy is not.<ref name=”domino” /> On the other hand, overfitting results in models that have lower bias but increased variance.<ref name=”ibm” /> [[File:Underfitting_overfitting_example.png|right|400px|thumb|caption|Figure illustrating underfitting versus overfitting<ref name=“img”>''Model Fit: Underfitting vs. Overfitting.'' Amazon Web Services. https://docs.aws.amazon.com/machine-learning/latest/dg/model-fit-underfitting-vs-overfitting.html</ref>]]Both overfitting and underfitting mean the model cannot establish the dominant pattern within the training data and, as a result, cannot generalize well to new data. This leads us to the concept called the [https://en.wikipedia.org/wiki/Bias%E2%80%93variance_tradeoff bias-variance tradeoff], which describes the need to balance between underfitting and overfitting when one is devising a model that performs well; you are essentially trading off between the bias and variance components of a model’s error so that neither becomes overwhelming.<ref name=”domino” /> Tuning a model away from either underfitting or overfitting pushes it closer towards the other issue.	+	With this in mind, one may logically think that ending the training process earlier, known as “early stopping,” or reducing complexity in the model would prevent overfitting; however, pausing training too early or excluding too many important features may result in the opposite problem: underfitting.<ref name=”ibm” /> Underfitting describes a model which does not capture the underlying relationship in the dataset which it was trained on.<ref name=”domino”> ''What is Underfitting in Machine Learning?'' Domino Data Lab. https://domino.ai/data-science-dictionary/underfitting</ref> While not training for long enough or being trained with poorly chosen [https://en.wikipedia.org/wiki/Hyperparameter_(machine_learning) hyperparameters] does lead to underfitting, the most common reason that models underfit is because they exhibit too much bias.<ref name=”domino” /> Basically, an underfit model will exhibit high bias and low variance, meaning it will generate reliably inaccurate predictions - while reliability is desirable, inaccuracy is not.<ref name=”domino” /> On the other hand, overfitting results in models that have lower bias but increased variance.<ref name=”ibm” /> [[File:Underfitting_overfitting_example.png|right|400px|thumb|caption|Figure illustrating underfitting versus overfitting<ref name=“img”>''Model Fit: Underfitting vs. Overfitting.'' Amazon Web Services. https://docs.aws.amazon.com/machine-learning/latest/dg/model-fit-underfitting-vs-overfitting.html</ref>]]Both overfitting and underfitting mean the model cannot establish the dominant pattern within the training data and, as a result, cannot generalize well to new data. This leads us to the concept called the [https://en.wikipedia.org/wiki/Bias%E2%80%93variance_tradeoff bias-variance tradeoff], which describes the need to balance between underfitting and overfitting when one is devising a model intended to perform well; you are essentially trading off between the bias and variance components of a model’s error so that neither becomes overwhelming.<ref name=”domino” /> Tuning a model away from either underfitting or overfitting pushes it closer towards the other issue.
	== How to Detect Overfit Models ==		== How to Detect Overfit Models ==
Line 18:		Line 18:
	=== Early-stopping ===		=== Early-stopping ===
−	[[File:Early_stopping_figure.png|right|700px|thumb|caption|Validation error vs testing error <ref name="ying">Ying, X. (2019). An Overview of Overfitting and its Solutions. ''2018 International Conference on Computer Information Science and Application Technology'', 1168(2), 1-7. https://doi.org/10.1088/1742-6596/1168/2/022022</ref>]]As mentioned earlier, this method involves pausing training before the model starts learning unnecessary noise in the training data. The phenomenon known as the “learning speed slow-down,” which means that the accuracy of algorithms stops improving after some point (or even gets worse due to noise-learning), can be avoided in this way.<ref name="ying" /> As shown in the figure to the right, where the horizontal axis is epoch, and the vertical axis is error, the blue line shows the training era and the red line shows the validation error. If the model continues learning after the exclamation point, the validation error will increase while the training error will continue decreasing; stopping learning before the point is underfitting and stopping learning after is overfitting - one should aim to find the exact point to stop training, striking the perfect balance between underfitting and overfitting.<ref name="ying" />	+	[[File:Early_stopping_figure.png|right|700px|thumb|caption|Validation error vs testing error <ref name="ying">Ying, X. (2019). An Overview of Overfitting and its Solutions. ''2018 International Conference on Computer Information Science and Application Technology'', 1168(2), 1-7. https://doi.org/10.1088/1742-6596/1168/2/022022</ref>]]As mentioned earlier, this method involves pausing training before the model starts learning unnecessary noise in the training data. The phenomenon known as the “learning speed slow-down,” which means that the accuracy of algorithms stops improving after some point (or even gets worse due to noise-learning), can be avoided in this way.<ref name="ying" /> As shown in the figure to the right, where the horizontal axis is epoch, and the vertical axis is error, the blue line shows the training error and the red line shows the validation error. If the model continues learning after the exclamation point, the validation error will increase while the training error will continue decreasing; stopping learning before the point is underfitting and stopping learning after is overfitting - one should aim to find the exact point to stop training, striking the perfect balance between underfitting and overfitting.<ref name="ying" />
	=== Expansion of the training data ===		=== Expansion of the training data ===
Line 27:		Line 27:
	== Recent Research ==		== Recent Research ==
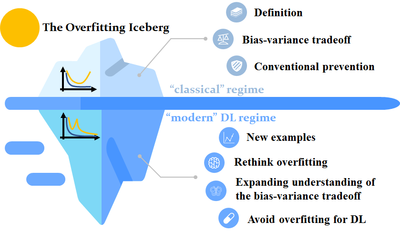
−	Overfitting, as a conventional and important topic of machine learning, has been well-studied with many fundamental theories and empirical evidence resulting from work done on this topic. However, with recent breakthroughs in [https://en.wikipedia.org/wiki/Deep_learning deep learning] (DL), machine learning practitioners have observed phenomena that seem to contradict or cannot be completely account for by the “classical” overfitting theory.<ref name="classic">Fang C, et al. (2020, Aug 31). ‘’4 - The Overfitting Iceberg.’’ Machine Learning | Carnegie Mellon University. https://blog.ml.cmu.edu/2020/08/31/4-overfitting/</ref> This “classical” overfitting theory can be summarized as believing that overfitting happens when a model is too complex and achieves much worse accuracy on new data than on the training data; this conventional understanding includes the bias-variance tradeoff where one needs to find the “sweet spot” between underfitting and overfitting.<ref name="classic" /> In the "classical" regime, one would want to avoid having zero error on training data as this was seen as equivalent to overfitting; however, in the age of DL, it has been widely observed that very complex neural networks trained to exactly fit the training data (traditionally seen as overfit models) often obtain high accuracy on new data as well, despite the bias-variance tradeoff concept implying that a model should balance underfitting and overfitting for good performance.<ref name="classic" /> Contradictions like these, in the age of deep learning, lead us to rethink the established definition of overfitting. This idea of our present understanding on overfitting not accounting for everything can be visualized by thinking of current knowledge on overfitting as just the “tip of the iceberg,” with the “underwater” part of the iceberg containing ideas not fully understood.<ref name="classic" />	+	Overfitting, as a conventional and important topic of machine learning, has been well-studied with many fundamental theories and empirical evidence resulting from work done on this topic. However, with recent breakthroughs in [https://en.wikipedia.org/wiki/Deep_learning deep learning] (DL), machine learning practitioners have observed phenomena that seem to contradict or are unable to be completely accounted for by the “classical” overfitting theory.<ref name="classic">Fang, C., Ding, J., Huang, Q., Tong, T., & Sun Y. (2020, Aug 31). ''4 - The Overfitting Iceberg.''
		+	Machine Learning | Carnegie Mellon University. https://blog.ml.cmu.edu/2020/08/31/4-overfitting/</ref> This “classical” overfitting theory can be summarized as believing that overfitting happens when a model is too complex and achieves much worse accuracy on new data than on the training data; this conventional understanding includes the bias-variance tradeoff where one needs to find the “sweet spot” between underfitting and overfitting.<ref name="classic" /> In the "classical" regime, one would want to avoid having zero error on training data as this was seen as equivalent to overfitting; however, in the age of DL, it has been widely observed that very complex neural networks trained to exactly fit the training data (traditionally seen as overfit models) often obtain high accuracy on new data as well, despite the bias-variance tradeoff concept implying that a model should balance underfitting and overfitting for good performance.<ref name="classic" /> Contradictions like these, in the age of deep learning, lead us to rethink the established definition of overfitting. This idea of our present understanding of overfitting not accounting for everything can be visualized by thinking of current knowledge on overfitting as just the “tip of the iceberg,” with the “underwater” part of the iceberg containing ideas not fully understood.<ref name="classic" />
	[[File:Overfitting_iceberg.png|right|400px|thumb|caption|The Overfitting Iceberg <ref name="classic" />]]		[[File:Overfitting_iceberg.png|right|400px|thumb|caption|The Overfitting Iceberg <ref name="classic" />]]
	== References ==		== References ==
	<references />		<references />

---

Latest revision as of 07:27, 22 October 2022

By Thomas Zhang

Overfitting is a phenomenon in machine learning which occurs when a learning algorithm fits too closely (or even exactly) to its training data, resulting in a model that is unable to make accurate predictions on new data.^[1] More generally, it means that a machine learning model has learned the training data too well, including “noise,” or irrelevant information, and random fluctuations, leading to decreased performance when presented with new data. This is a major problem as the ability of machine learning models to make predictions/decisions and classify data has many real-world applications; overfitting interferes with a model’s ability to generalize well to new data, directly affecting its ability to do the classification and prediction tasks it was intended for.^[1]

Background/History

The term “overfitting” first originated in the field of statistics, with this subject being extensively studied in the context of regression analysis and pattern recognition; however, with the arrival of artificial intelligence and machine learning, this phenomenon has been subject to increased attention due to its important implications on the performance of AI models.^[2] Since its early days, the concept has evolved significantly, with researchers continuously endeavoring to develop methods to mitigate overfitting’s adverse effects on the accuracy of models and their ability to generalize.^[2]

Overfitting

Overfitting occurs when a machine learning model captures not only the underlying patterns in the training data, but the random noise or errors as well. This tends to happen when the model trains for too long on sample data or when the model is too complex. When a model is excessively trained on a limited dataset, it leads to the model memorizing the specific data points rather than learning the underlying patterns of the dataset.^[2] Complex models with a large number of parameters are also conducive for overfitting in that they have the capacity to learn intricate details, including noise, from the training data.^[2]

With this in mind, one may logically think that ending the training process earlier, known as “early stopping,” or reducing complexity in the model would prevent overfitting; however, pausing training too early or excluding too many important features may result in the opposite problem: underfitting.^[1] Underfitting describes a model which does not capture the underlying relationship in the dataset which it was trained on.^[3] While not training for long enough or being trained with poorly chosen hyperparameters does lead to underfitting, the most common reason that models underfit is because they exhibit too much bias.^[3] Basically, an underfit model will exhibit high bias and low variance, meaning it will generate reliably inaccurate predictions - while reliability is desirable, inaccuracy is not.^[3] On the other hand, overfitting results in models that have lower bias but increased variance.^[1]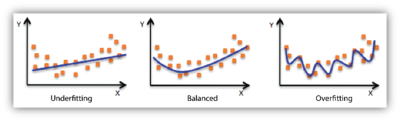 Both overfitting and underfitting mean the model cannot establish the dominant pattern within the training data and, as a result, cannot generalize well to new data. This leads us to the concept called the bias-variance tradeoff, which describes the need to balance between underfitting and overfitting when one is devising a model intended to perform well; you are essentially trading off between the bias and variance components of a model’s error so that neither becomes overwhelming.^[3] Tuning a model away from either underfitting or overfitting pushes it closer towards the other issue.

How to Detect Overfit Models

The performance (accuracy) of a machine learning model is assessed to help one determine if there are any issues, like overfitting or underfitting, in the model; k-fold cross-validation is one of the most popular techniques to assess model fitness.^[1] In this procedure, we divide the dataset into k groups and take each unique group as a test data set with the remaining groups composing the training data set associated with that test data set.^[5] We then fit a model on each training set and evaluate it on the corresponding test set, retaining the evaluation score and discarding the model.^[5] When all evaluations have been done (there should have been k of them), the performance of the overall model can be summarized with the obtained scores; this often means averaging the evaluation scores to assess the overall model’s performance.^[5] Additionally, it is generally good practice to include a measure of the variance of the scores, such as the standard deviation or standard error. ^[5]

How to Avoid Overfitting

Below are some techniques that one can use to prevent overfitting:

Early-stopping

As mentioned earlier, this method involves pausing training before the model starts learning unnecessary noise in the training data. The phenomenon known as the “learning speed slow-down,” which means that the accuracy of algorithms stops improving after some point (or even gets worse due to noise-learning), can be avoided in this way.^[6] As shown in the figure to the right, where the horizontal axis is epoch, and the vertical axis is error, the blue line shows the training error and the red line shows the validation error. If the model continues learning after the exclamation point, the validation error will increase while the training error will continue decreasing; stopping learning before the point is underfitting and stopping learning after is overfitting - one should aim to find the exact point to stop training, striking the perfect balance between underfitting and overfitting.^[6]

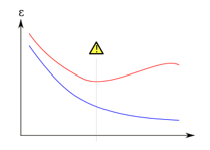
Expansion of the training data

Expanding the training set to include more data can increase the accuracy of the model by providing more opportunities to parse out the dominant, underlying relationship in the training data.^[1] However, in many cases a model’s performance is not only significantly affected by the quantity of the training dataset but the quality of that data as well (especially in the area of supervised learning).^[6] This method of expanding the training data is more effective when clean, relevant data is injected into the model; otherwise, you could just continue adding more complexity to the model, causing it to overfit.^[1]

Regularization

Generally, the model output can be affected by multiple features (more features means a more complicated model); however, overfitting models tend to take all the features into account, even though some of them have a very limited effect on the final output - in fact, some of them might be noises which are meaningless to the model output.^[6] In response to the complexity in a model making it overfit, we need to limit the effect of the useless features. However, because we do not always know which features are useless, we instead use regularization methods; regularization applies a “penalty” to the input parameters (features) with the larger coefficients, ultimately limiting the variance in the model. ^[1] Though there are multiple regularization methods (e.g., lasso regularization, ridge regression, and dropout), they all seek to identify and reduce the noise within the data.^[1]

Recent Research

Overfitting, as a conventional and important topic of machine learning, has been well-studied with many fundamental theories and empirical evidence resulting from work done on this topic. However, with recent breakthroughs in deep learning (DL), machine learning practitioners have observed phenomena that seem to contradict or are unable to be completely accounted for by the “classical” overfitting theory.^[7] This “classical” overfitting theory can be summarized as believing that overfitting happens when a model is too complex and achieves much worse accuracy on new data than on the training data; this conventional understanding includes the bias-variance tradeoff where one needs to find the “sweet spot” between underfitting and overfitting.^[7] In the "classical" regime, one would want to avoid having zero error on training data as this was seen as equivalent to overfitting; however, in the age of DL, it has been widely observed that very complex neural networks trained to exactly fit the training data (traditionally seen as overfit models) often obtain high accuracy on new data as well, despite the bias-variance tradeoff concept implying that a model should balance underfitting and overfitting for good performance.^[7] Contradictions like these, in the age of deep learning, lead us to rethink the established definition of overfitting. This idea of our present understanding of overfitting not accounting for everything can be visualized by thinking of current knowledge on overfitting as just the “tip of the iceberg,” with the “underwater” part of the iceberg containing ideas not fully understood.^[7]

References